반응형
그래프란?
그래프는 정점(Vertex)과 간선(Edge)으로 이루어진 자료구조이다.
정확히는 정점(Vertex)간의 관계를 표현하는 조직도라고 볼 수 있다.
이러한 면에서 트리는 그래프의 일종인 셈이다.
하지만 그래프는 트리와는 달리 정점마다 간선이 있을 수도 있고 없을 수도 있으며, 루트노드와 부모와 자식이라는 개념이 존재하지 않는다.
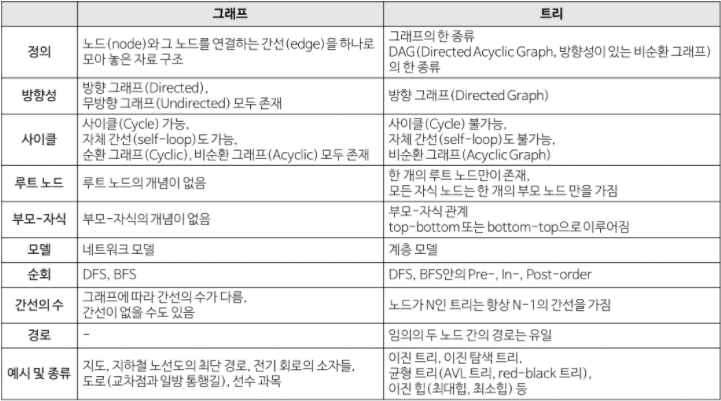
그래프와 트리의 차이점에 대해서는 아래의 표로 좀 더 자세하게 설명하겠다.
그래프와 트리의 차이
그래프와 관련된 용어
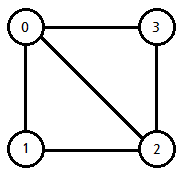
- 정점(Vertex) : 노드(node) 라고도 하며 정점에는 데이터가 저장된다. (0, 1, 2, 3)
- 간선(Edge) : 정점(노드)를 연결하는 선으로 link, branch 라고도 부른다.
- 인접 정점(adjacent Vertex) : 간선에 의해 직접 연결된 정점 (0과 2은 인접정점)
- 단순 경로(simple path) : 경로 중에서 반복되는 정점이 없는 경우. 한붓그리기와 같이 같은 간선을 지나가지 않는 경로 ( 0->3->2->1 은 단순경로 )
- 차수(degree) : 무방향 그래프에서 하나의 정점에 인접한 정점의 수 (0의 차수는 3)
- 진출 차수(in-degree) : 방향 그래프에서 외부로 향하는 간선의 수
- 진입 차수(out-degree) : 방향 그래프에서 외부에서 들어오는 간선의 수
- 경로 길이(path length) : 경로를 구성하는데 사용된 간선의 수
- 사이클(cycle) : 단순 경로의 시작 정점과 종료 정점이 동일한 경우
그래프의 구현 방법
그래프를 구현하는 방법에는 인접행렬과 인접리스트 방식이 있다. 두 개의 구현방식은 각각의 상반된 장단점을 가지고 있다.
- 인접행렬 방식
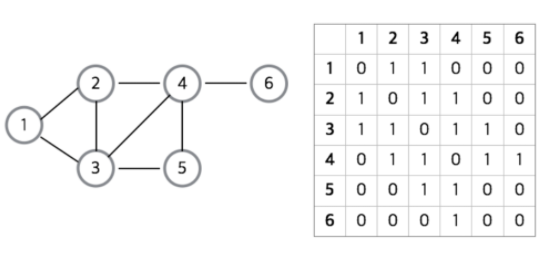
인접행렬은 그래프의 노드를 2차원 배열로 만든 것이다.
노드들 간에 직접 연결이 되어있으면 1을, 아니면 0을 넣어서 행렬을 완성시킨 것이다. - 인접행렬의 장점
- 2차원 배열 안에 모든 정점들의 간선 정보가 담겨있기 때문에 두 정점에 대한 연결 정보를 조회할 때 O(1) 의 시간복잡도면 가능하다.
- 인접리스트에 비해 구현이 쉽다.
- 인접행렬의 단점
- 모든 정점에 대해 간선 정보를 대입해야 하므로 $O(n^2)$ 의 시간복잡도가 소요된다.
- 무조건 2차원 배열이 필요하기 때문에 필요 이상의 공간이 낭비된다.
- 인접리스트 방식
인접리스트는 그래프의 노드를 리스트로 표현한 것이다.
주로 정점의 리스트 배열을 만들어 관계를 설정하며 노드들 간에 직접 연결이 되어있으면 해당 노드의 인덱스에 그 노드를 삽입해주면 된다.
즉, 1에는 2와 3이 직접 연결되어 있기 때문에 배열의 1번째 칸에 2와 3을 넣어준다.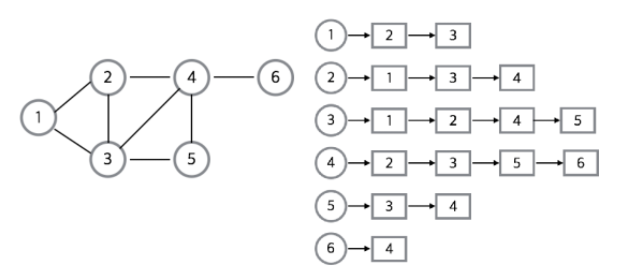
- 인접리스트의 장점
- 정점들의 연결 정보를 탐색할 때 O(n) 시간이면 가능하다.
- 필요한 만큼의 공간만 사용하기 때문에 공간의 낭비가 적다.
- 인접리스트의 단점
- 특정 두 점이 연결되었는지 확인하려면 인접행렬에 비해 시간이 오래걸린다. (O(E) 시간 소요. E는 간선의 개수)
- 구현이 비교적 어렵다.
그래프의 종류
- 무방향 그래프(Undirected Graph)
무방향 그래프는 두 정점을 연결하는 간선에 방향이 없는 그래프이다.
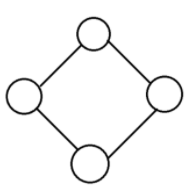
- 방향 그래프(Directed Graph)
방향 그래프는 두 정점을 연결하는 간선에 방향이 존재하는 그래프이다.
간선의 방향으로만 이동할 수 있다.
- 가중치 그래프(Weighted Graph)
가중치 그래프는 간선에 가중치(비용)가 할당된 그래프로, 두 정점을 이동할 때 비용이 드는 그래프이다.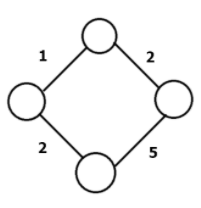
- 연결 그래프(Connected Graph)
무방향 그래프에 있는 모든 정점 쌍에 대해서 항상 경로가 존재하는 그래프
즉, 노드들이 하나도 빠짐없이 간선에 의해 연결되어 있는 그래프로 트리(Tree)가 대표적인 예이다.
- 비연결 그래프(Disconnected Graph)
무방향 그래프에서 특정 정점 사이에 경로가 존재하지 않는 그래프
즉, 노드들 중 간선에 의해 연결되어 있지 않은 그래프이다.
- 완전 그래프(Complete graph)
그래프의 모든 정점이 서로 연결되어 있는 그래프이다. (인접 연결)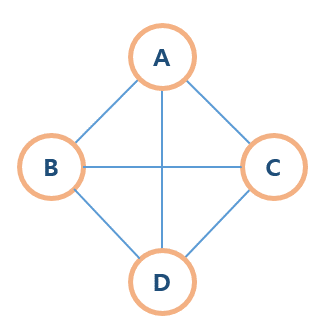
- 순환그래프(Cycle)
단순 경로에서 시작 정점과 도착 정점이 동일한 그래프이다. (A에서 시작-> A에서 끝 가능)
- 비순환그래프(Acyclic Graph)
사이클 그래프를 제외한 그래프로, 사이클이 없는 그래프이다.
- 신장트리(Spanning Tree)

원래 그래프의 모든 노드가 연결되어 있으면서, 트리의 속성을 만족하는 그래프
트리의 속성을 만족하기 때문에 사이클이 존재하면 안된다.
- 최소 신장트리(Minimum Spanning Tree)

신장트리(Spanning Tree)중 간선의 가중치 합이 최소인 신장 트리
면접에서 나올 수 있는 질문
- 인접행렬과 인접리스트의 차이점과 각각의 장단점에 대해 이야기 해보세요
- 연결그래프와 완전그래프의 차이점에 대해 이야기 해보세요
- (원래 그래프의 그림을 주고) 이 그래프로 신장 트리 N개를 만들어 보세요
- 최소신장트리를 찾을 수 있는 알고리즘에 대해 설명해주세요
- -> https://velog.io/@dnjscksdn98/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EC%B5%9C%EC%86%8C-%EC%8B%A0%EC%9E%A5-%ED%8A%B8%EB%A6%AC 참고
참고 자료
기여자
반응형
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 이진탐색트리 (0) | 2023.02.16 |
|---|---|
| [자료구조] 힙(Heap) 에 대하여 (0) | 2023.02.16 |
| [자료구조] 스택(Stack), 큐(Queue) (0) | 2023.02.15 |
| [자료구조] 트리(Tree) (0) | 2023.02.15 |
| [자료구조] 배열과 연결리스트 (Array & LinkedList) (0) | 2021.05.21 |



