CS/알고리즘
[알고리즘] 힙 정렬(Heap Sort)
안드선생
2023. 2. 20. 15:40
반응형
힙 정렬이란?
힙 정렬(Heap Sort)이란 최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법으로서,
내림차순 정렬을 위해서는 최대 힙을 구성하고
오름차순 정렬을 위해서는 최소 힙을 구성한다.
힙 정렬은 1964년 J.W.J 윌리엄스에 의해 발명되었고, 같은 해 R.W. 플로이드가 제자리 정렬을 할 수 있는 개선판을 출판하였고 이 방법이 바로 트리정렬 알고리즘을 이용한 방식이다.
힙 정렬 시뮬레이션
아래의 그림은 힙 정렬을 시뮬레이션한 그림이다.
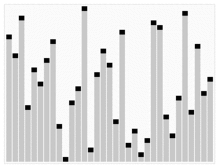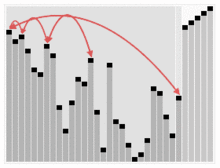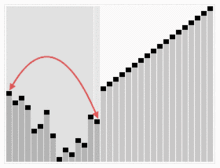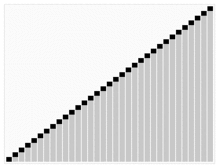
추가로 힙 정렬을 숫자와 함께 보고 싶다면 아래의 사이트를 가보는 것도 추천한다.
힙 정렬 과정
힙 정렬 과정을 알기 위해선 힙 자료구조에 대한 선행 공부가 필수적이다.
만약 힙에 대한 자료구조를 모른다면 [자료구조] 힙 포스팅을 한번 보고오도록 하자.
이제 힙 자료구조를 안다고 가정하고 과정을 설명해보고자 한다.
- n개의 노드에 대한 완전 이진 트리를 구성한다. 이때 루트 노드부터 부모노드, 왼쪽 자식노드, 오른쪽 자식노드 순으로 구성한다.
- 최대 힙을 구성한다. 최대 힙이란 부모노드가 자식노드보다 큰 트리를 말하는데,
단말 노드를 자식노드로 가진 부모노드부터 구성하며 아래부터 루트까지 올라오며 순차적으로 만들어 갈 수 있다. - 가장 큰 수(루트에 위치)를 가장 끝의 노드와 교환한다.
- 2와 3을 반복한다.
위의 알고리즘을 이제 시뮬레이션을 통하여 확인해보자.
[6, 5, 3, 1, 8, 7, 2, 4] 의 배열을 오름차순으로 정렬하는 문제가 주어졌다고 가정하자.
맨 위에서 설명한 것과 같이 오름차순 정렬은 최대 힙을 구성하여 정렬을 수행한다.

- 먼저 이진 탐색트리를 만들며 최대 힙을 구현한다.
- 그 후 최대 힙의 최대 루트 노드를 배열의 마지막 자리 원소로 고정하고 트리에서 마지막 노드와 자리를 바꾼다.
- 이 과정을 모든 자리가 고정될 때까지 최대 힙을 만들고 루트 노드를 배열의 마지막 자리 원소로 만드는 과정을 반복하며 정렬을 수행한다.
힙 정렬 시간 복잡도
힙 구현 포스팅에서도 알아봤듯이, 최대 힙으로 만드는 과정(heapify)의 시간 복잡도는 이다.
이 heapify의 과정이 n개의 원소를 다 정렬할 때까지 반복되므로 최종 힙 정렬의 시간 복잡도는 이 된다.
힙 정렬 구현 코드
// c++ 로 구현한 힙 정렬
#include <iostream>
using namespace std;
// i 노드가 가장 큰 노드인 힙트리를 만들기 위한 함수
// 힙 사이즈는 n
void heapify(int arr[], int n, int i)
{
int largest = i; // 루트를 가장 큰 노드로 초기 설정
int l = 2 * i + 1; // left
int r = 2 * i + 2; // right
// 왼쪽 자식 노드가 가장 큰 노드보다 클 때
if (l < n && arr[l] > arr[largest])
largest = l;
// 오른쪽 자식 노드가 가장 큰 노드보다 클때
if (r < n && arr[r] > arr[largest])
largest = r;
// 만약, 가장 큰 노드가 루트가 아니면 스왑
if (largest != i) {
swap(arr[i], arr[largest]);
// 재귀적으로 서브트리를 힙화 한다.
heapify(arr, n, largest);
}
}
// 힙 정렬 함수
void heapSort(int arr[], int n)
{
// 힙을 구성 (배열 재 정렬)
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
// 하나씩 힙에서 원소를 추출
for (int i = n - 1; i > 0; i--) {
// 루트노드를 끝 노드로 이동
swap(arr[0], arr[i]);
// 줄어든 힙에서 최대 힙 구성
heapify(arr, i, 0);
}
}
// n 크기의 배열을 출력하는 코드
void printArray(int arr[], int n) {
for (int i = 0; i < n; ++i)
cout << arr[i] << " ";
cout << "\n";
}
int main() {
int arr[] = { 12, 11, 13, 5, 6, 7 };
int n = sizeof(arr) / sizeof(arr[0]);
heapSort(arr, n);
cout << "정렬된 배열은 : \n";
printArray(arr, n);
}
힙 정렬 특징 정리
- 정렬을 위한 추가적인 메모리가 필요하지 않다. (제자리 정렬 가능)
- 최선, 평균, 최악의 경우의 모두 heapify 과정이 필요하기 때문에 nlogn 을 보장한다.
- 데이터의 순서를 보장하지 못하는 불안정(unstable)정렬이다.
- 힙정렬과 퀵정렬을 비교해보면 똑같은 nlogn 이지만 컴퓨터의 하드웨어 구조상 퀵정렬이 실제로는 더 빠르다고 한다. 이유는 퀵 정렬의 경우는 대개 원소들끼리 근접한 메모리 영역에 붙어 있는 배열을 사용하기 때문에 일반적으로 캐시 친화적이지만
힙정렬의 원소들은 좀 더 흩어져 있는 경우가 많아서 캐시 친화도가 떨어지는 문제가 있고
힙정렬은 일반적으로 포인터 연산을 많이 사용하기 때문에 거기에 걸리는 오버헤드도 무시할 수는 없는 수준이기 때문이다.
나올 수 있는 면접 질문
- 힙 정렬의 과정을 말씀해 주세요.
- 힙 정렬의 시간복잡도는 어떻게 되나요? 왜 그러한 시간복잡도가 나오나요?
- 힙 정렬과 퀵 정렬 어떤게 더 빠를까요?
참고
반응형