[자료구조] 해시 테이블
해시 테이블
해시 테이블이란 연관배열 구조를 이용하여 (Key, Value)로 데이터를 저장하는 자료구조로,
빠르게 데이터를 검색할 수 있는 자료구조이다.
기본 연산으로는 탐색, 삽입, 삭제가 있다.
TIP
연관배열 구조란 키(Key) 1개와 값(Value) 1개가 1:1로 연관되어 있는 자료구조이다.
해시 테이블 연산
① 삽입

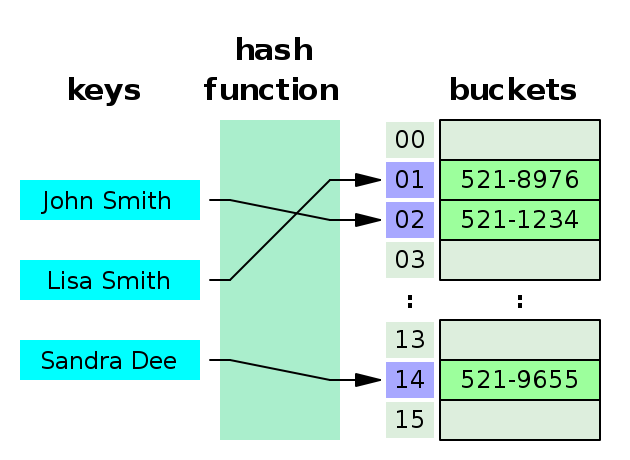
해시 테이블에서 자료를 저장하기 위해서는 해시 함수(Hash Function)를 통하여
키(Key)를 -> 해시(Hash)로 변경해야 한다.
위 사진의 해시 함수는 input key를 7로 나눈 나머지이므로
첫 번째 데이터의 키는 76, 해시는 6이 된다.
미리 준비해놓은 0 ~ 6의 저장소 중에 맞는 해시값을 찾아 해당 값을 저장한다.
해시 함수로 해시를 얻어내는 과정에서 서로 다른 key 값이 같은 hash로 변환되는 문제가 발생할 수 있는데
이를 해시 충돌이라고 하며 이 문제를 해결해야 한다.
(해결 방법은 아래에서 소개한다.)
해시테이블 삽입단계의 시간복잡도는 O(1)이다.
유일한 키를 해시함수의 결과로 해시와 키를 저장소에 넣으면 되기 때문이다.
하지만 모든 bucket에서 충돌이 일어날 경우, 최악의 경우 O(n)이 될 수 있다.
② 삭제
저장되어 있는 값을 삭제할 때는 해당 key와 매칭되는 값을 찾아서 삭제하면 된다.
삭제도 마찬가지로 시간복잡도는 O(1)이다.
유일한 키 값을 해시함수의 결과로 나온 해시에 매칭되는 값을 삭제하면 되기 때문이다.
하지만 모든 bucket에서 충돌이 일어날 경우, 최악의 경우로 O(n)이 될 수 있다.
③ 탐색
키로 값을 찾아내는 과정으로, 삭제 연산과 과정이 비슷하다.
- 키로 hash를 구한다.
- hash로 키를 구한다.
저장단계의 시간복잡도도 마찬가지로 O(1)이다.
유일한 키 값을 해시함수의 결과로 나온 해시에 매칭되는 값을 찾으면 되기 때문이다.
하지만 모든 bucket에서 충돌이 일어날 경우, 최악의 경우로 O(n)이 될 수 있다.
TIP
위의 모든 시간복잡도는 해시함수의 시간복잡도가 함께 고려되지 않는다.
해시 충돌
해시테이블은 세가지 연산 과정에서 모두 평균적으로 O(1)의 시간복잡도를 가지기 때문에
자료구조의 효율성 측면에서 좋은 자료구조라고 볼 수 있다.
하지만 발생할 수 있는 문제는 바로 해시 충돌이다.
해시 충돌을 해결하기 위한 방법은 크게 2가지가 있다.
① 체이닝(Chaining)

위에 사진에서 Sandra Dee가 삽입하는데, John Smith과 충돌이 일어나게 된다.
그럴때 John Smith의 뒤에 Sandra Dee를 연결시키는 방법이 바로 체이닝 기법이다.
※ 체이닝의 장점
- 한정된 저장소를 효율적으로 사용 가능하다.
- 해시 함수를 선택하는 중요성이 상대적으로 적다.
- 상대적으로 적은 메모리를 사용한다. (미리 공간 잡을 필요X)
※ 체이닝의 단점
- 한 Hash에 자료들이 계속 연결된다면(쏠림현상) 검색 효율이 낮아진다.
- 외부 저장 공간을 사용한다.
- 외부 저장 공간 작업을 추가로 해야한다.
체이닝의 시간복잡도
테이블의 저장소 길이를 n, 키의 수를 m이라고 했을 때,
평균적으로 저장소에서 1개의 hash당 m/n개의 키가 들어있다. 이를 α라고 하자.
삽입연산
충돌이 일어났을 때, 해시가 가진 연결리스트의 Head에 자료를 저장할 경우, O(1)의 시간복잡도를 가진다.
하지만 Tail에 자료를 저장할 경우, O(α)의 시간 복잡도를 가진다.
한개의 해시에 모든 자료가 연결되어있는 최악의 경우, O(n)의 시간복잡도를 가진다.
삭제연산 & 탐색연산
산출된 Hash의 연결리스트를 차례대로 살펴보아야 하므로 O(α)의 시간 복잡도를 가진다.
한 개의 해시에 모든 자료가 연결되어 있는 최악의 경우 O(n)의 시간복잡도를 가진다.
② 개방주소법(Open Addressing)
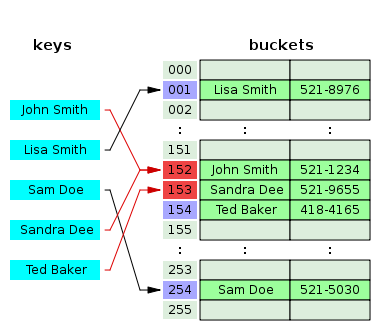
개방주소법은 비어있는 해시를 찾아 해시를 변경하여 데이터를 저장하는 기법이다.
위 사진에서 Sandra Dee가 삽입될 때 해시가 John Smith로 이미 채워져 있다.
그렇게 되면 바로 다음 빈 Hash에 Sandra를 저장한다.
그 다음 Ted Baker의 해시도 Sandra Dee가 저장되어 있기 때문에
그 다음 빈 해시에 Ted를 저장한다.
바로 다음 빈 해시에 저장하는 것은 한 예시이며,
비어있는 해시를 찾는 규칙은 총 3가지가 존재한다.
- 선형 탐색(Linear Probing): 다음 해시나 n개를 건너뛰어 비어있는 해시 에 데이터를 저장
- 제곱 탐색(Quadratic Probing): 충돌이 일어난 해시의 제곱을 한 해시 에 데이터를 저장
- 이중 해시(Double Hashing): 다른 해시함수를 한번 더 적용한 해시 에 데이터를 저장
- 또 다른 저장공간 없이 해시테이블 내에 데이터 저장 및 처리 가능
- 또 다른 저장공간에서의 추가적인 작업 없음
- 해시 함수의 성능에 전체 해시테이블의 성능이 갈림
- 데이터의 길이가 늘어나면 그에 해당하는 저장소를 마련해야함
개방주소법의 시간복잡도
삽입, 삭제, 검색 모두 해시함수를 통해 얻은 Hash가 비어있지 않으면 다음 버킷을 찾아가야 한다.
그러므로 찾아가는 횟수가 많아질수록, 시간 복잡도가 증가하게 된다.
따라서, 최상의 경우 O(1)이며 최악의 경우 O(n)이다.
결국, 개방주소법에서는 비어있는 공간을 확보하는 것이 필요하다.
(저장소가 어느 정도 채워지면 저장소의 사이즈를 늘려주어야 한다.)
해시 테이블의 단점
- 순서가 있는 배열에 어울리지 않음
- 공간 효율성이 떨어짐
- Hash Function(해시 함수)의 의존도가 높음